LLM KV Cache

type: Post
status: Published
date: 2024/03/13
category: Technical Sharing

KV-Cache

KV-Cache is a commonly used feature in Transformers, applied to accelerate inference in Decoder architectures.

Self-Attention Process Without KV-Cache

The following process is adapted from Zhihu [1].

For a given text input, the computation proceeds as follows:

1. First, input the embedding of a token, with shape [1, emb_size].

After applying the formula, we obtain the attention vector (for simplicity, $\sqrt{d}$ is omitted):

$$ Att_1(Q,K,V)=softmax(\frac{Q_1,K^T_1}{\sqrt{d}})\overset{\rightarrow}{V} $$

2. Input the second token.

Here, the attention calculation formula is:

$$ \begin{align}Att_2(Q,K,V)&=softmax\left(\left[\begin{matrix}Q_1K_1^T -\infty \Q_2K_1^T Q_2K_2^T\end{matrix}\right]\right)\left[\begin{matrix}\overset{\rightarrow}{V_1} \ \overset{\rightarrow}{V_2}\end{matrix}\right] \ &=\left(\left[\begin{matrix}softmax(Q_1K_1^T)\overset{\rightarrow}{V_1}+0 \ softmax(Q_2K_1^T)\overset{\rightarrow}{V_1} + softmax(Q_2K_2^T)\overset{\rightarrow}{V_2} \end{matrix}\right]\right)\end{align} $$

Thus, we can see:

$$ \begin{align}Att_1(Q,K,V)&=softmax(Q_1K_1^T)\overset{\rightarrow}{V_1} \ Att_2(Q,K,V)&=softmax(Q_2K_1^T)\overset{\rightarrow}{V_1} + softmax(Q_2K_2^T)\overset{\rightarrow}{V_2} \end{align} $$

Subsequent attention calculations follow the same logic:

$$ Att_i(Q,K,V)=\sum^i_{j=1}softmax(Q_iK^T_j)\overset{\rightarrow}{V_j} $$

From this, we can conclude:

1. The current computation method has a lot of redundancy and can be optimized.
2. Attention only depends on $Q_k$.
3. To infer the i-th character, only the previous i-1 are needed.

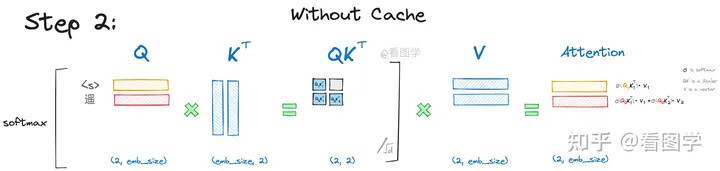
Inference Acceleration Diagram

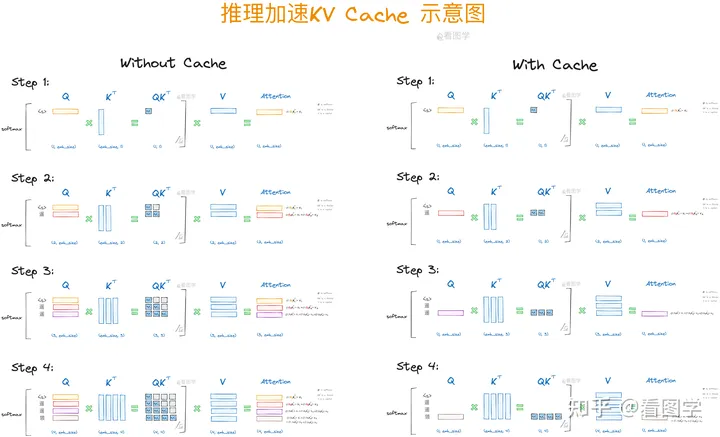
Reference

[1] https://zhuanlan.zhihu.com/p/662498827