大模型 KV Cache

type: Post status: Published date: 2024/03/13 category: 技术分享

KV-Cache

KV-Cache是目前Transformer常用的功能，应用于Decoder架构的推理加速。

Self-Attention 不带KV-Cache流程

以下流程来自知乎看图学[1]

对于一段文字输入，有以下计算过程：

1. 首先输入一个token的embedding，大小为[1, emb_size]

经过公式计算得出attention向量，这里为方便表示$\sqrt{d}$被省略

$$ Att_1(Q,K,V)=softmax(\frac{Q_1,K^T_1}{\sqrt{d}})\overset{\rightarrow}{V} $$

1. 输入第二个token

在这里可以发现，attention的计算公式为：

$$ \begin{align}Att_2(Q,K,V)&=softmax\left(\left[\begin{matrix}Q_1K_1^T -\infty \Q_2K_1^T Q_2K_2^T\end{matrix}\right]\right)\left[\begin{matrix}\overset{\rightarrow}{V_1} \ \overset{\rightarrow}{V_2}\end{matrix}\right] \ &=\left(\left[\begin{matrix}softmax(Q_1K_1^T)\overset{\rightarrow}{V_1}+0 \ softmax(Q_2K_1^T)\overset{\rightarrow}{V_1} + softmax(Q_2K_2^T)\overset{\rightarrow}{V_2} \end{matrix}\right]\right)\end{align} $$

因此可以发现：

$$ \begin{align}Att_1(Q,K,V)&=softmax(Q_1K_1^T)\overset{\rightarrow}{V_1} \ Att_2(Q,K,V)&=softmax(Q_2K_1^T)\overset{\rightarrow}{V_1} + softmax(Q_2K_2^T)\overset{\rightarrow}{V_2} \end{align} $$

随后的attention也同理可得

$$ Att_i(Q,K,V)=\sum^i_{j=1}softmax(Q_iK^T_j)\overset{\rightarrow}{V_j} $$

因此可以得出结论：

1. 当前计算方式存在大量冗余，计算量可以优化
2. Attention只与$Q_k$相关
3. 推理第i个字符只需要i-1即可

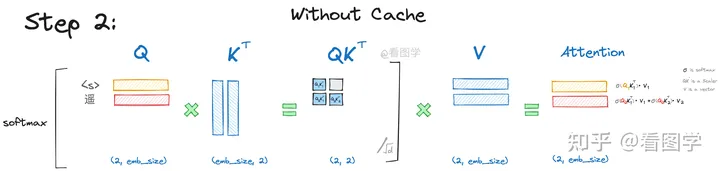
推理加速示意图

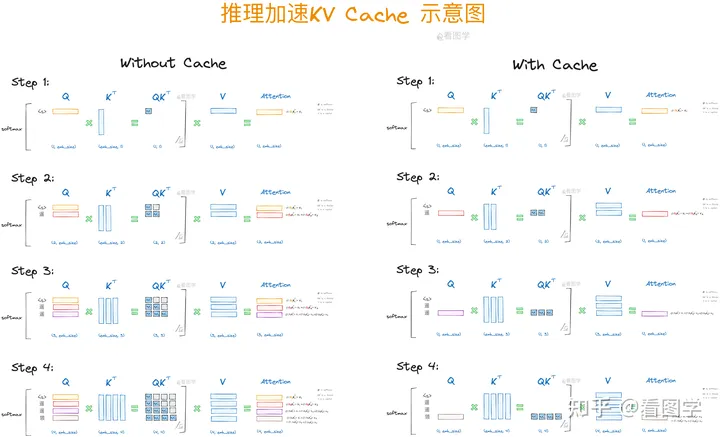
参考：

[1] https://zhuanlan.zhihu.com/p/662498827